数据结构 learn 学了差不多10多天的数据结构,还有很多小章节没学,但是收获还是挺大的。
线性表 线性表的顺序储存结构 说白了就是类似于结构体数组,或者直接就是数组,例子在c++ learn 文章的实战-通讯录管理资料。
优点:
无须为表中元素之间的逻辑关系而增加额外的储存空间。
可以快速的取表中任意位置的元素。
缺点
插入和删除操作需要移动大量元素
当线性表长度变化较大时,难以确定存储空间的容量
造成存储空间的“碎片”
线性表的链式存储结构 就是链表
单链表 主要学习如何生成链表,插入数据,头插法,尾插法,如何删除数据,如何删除链表。
自己写的一个例子
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 #include <stdio.h> #include <stdlib.h> typedef struct Node { int date; struct Node * next ; }Node,*List; void creathead (List *list ) *list = (List)malloc (sizeof (Node)); (*list )->next = NULL ; } int getlistlen (List head) int i=0 ; List p; p = head->next; while (p) { i++; p = p->next; } return i; } void creatlist1 (List head, int len) int i; List p,q; q = head; for (i = 0 ; i < len; i++) { p = (List)malloc (sizeof (Node)); p->date = i; q->next = p; q = p; } q->next = NULL ; } void creatlist2 (List head, int len) int i; List p, q; q = head; q->next = NULL ; for (i = 0 ; i < len; i++) { p = (List)malloc (sizeof (Node)); p->date = i; p->next = q->next; head->next = p; } } void getlist (List head, int len) int i; List p; p = head->next; for (i = 0 ; i < len; i++) { printf ("%d " , p->date); p = p->next; } } void deletelist (List head) List p, q; p = head->next; while (p) { q = p->next; free (p); p = q; } head->next = NULL ; } void delete_one (List head, int target) int len = getlistlen(head); if (target >= len||target < 0 ) { printf ("no" ); } else { List p,q; int i; p = head; for (i = 0 ; i < target; i++) { p = p->next; } q = p->next; p->next = q->next; free (q); } } void add_one (List head, int target,int num) int len = getlistlen(head); if (target > len || target < 0 ) { printf ("no" ); } else { List p, q; int i; p = head; for (i = 0 ; i < target; i++) { p = p->next; } q= (List)malloc (sizeof (Node)); q->date = num; q->next = NULL ; q->next = p->next; p->next = q; } } int main () List head; creathead(&head); creatlist1(head, 5 ); delete_one(head, 3 ); add_one(head, 3 , 3 ); add_one(head, 5 , 5 ); getlist(head, getlistlen(head)); deletelist(head); }
可以看到单链表的好处是可以随便插入和删除数据,而对整体产生较小影响。
静态链表 这个就是低级版的链表,用数组来实现,就是一个数据,然后跟一个值,这个值就是下个数据在数组中的下标,依次这样做,特别的是第一个元素和最后一个元素,不存数据。这种链表实际上了解一下思路就可以了,因为相对于动态链表,它的缺点还是比较明显。
如果用定义一个结构体数组来表示静态链表的话,第一个相当于是中间值,其指向一定是空区域,用来申请或者释放属于空间,最后一个相当于表头,用来从开头寻找到结尾,结尾的指向一定为0,用来判断数据长度。值得注意的是,这种静态链表,其数据位置是不会变的,变的只是他的下一个指向。
下面是我写的例子,只提供了插入,没提供删除,了解个思路就差不多了啦。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 #include <stdio.h> typedef struct { char num; int nextindex; }Statclist, Statclinklist[10 ]; char table[10 ] = { 'a' ,'b' ,'d' ,'e' ,'f' ,'g' };void initlist (Statclinklist exp ) int i; for (i = 0 ; i < 10 -1 ; i++) { exp [i].num = 0 ; exp [i].nextindex = i + 1 ; } for (i = 0 ; i < 7 ; i++) { exp [i+1 ].num = table[i]; } exp [10 -1 ].num = 0 ; exp [0 ].nextindex = 7 ; exp [6 ].nextindex = 0 ; exp [10 -1 ].nextindex = 1 ; } int getlen (Statclinklist exp ) int len=0 ; int index=exp [9 ].nextindex; while (index) { index = exp [index].nextindex; len++; } return len; } void putlist (Statclinklist exp ) int i,len; int index=9 ; len = getlen(exp ); for (i = 0 ; i <= len; i++) { printf ("%c" , exp [index].num); index = exp [index].nextindex; } } int statclinklistmalloc (Statclinklist exp ) int i; i = exp [0 ].nextindex; if (exp [0 ].nextindex) exp [0 ].nextindex = exp [i].nextindex; return i; } void add_one (Statclinklist exp , char ch,int in) int i, k, j; k = 9 ; if (in < 1 || in>getlen(exp )+1 ) { printf ("no" ); } i = statclinklistmalloc(exp ); if (i) { exp [i].num = ch; for (j = 1 ; j <= in - 1 ; j++) { k = exp [k].nextindex; } exp [i].nextindex = exp [k].nextindex; exp [k].nextindex = i; } } int main () Statclinklist exp ; initlist(exp ); add_one(exp , 'c' , 3 ); putlist(exp ); }
循环链表 没什么好说的,就是尾指针指向表头地址。
双向链表 就是在链表基础上加上一个可以向前访问的指针。
1 2 3 4 5 6 7 typedef struct Node { int date; struct Node * prior ; struct Node * next ; }Node, * List;
这种结构就可以从某个元素向两头访问,插入和删除会稍微复杂一点,因为有两个指针。
栈与队列 栈 先进后出
普通栈 最基本的栈,用一个固定长度数组实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 #include <stdio.h> #define max 10 typedef struct { int data[max]; int top; }Stack; void initStack (Stack *S) S->top = -1 ; } int getlen (Stack* S) return S->top; } void push (Stack *S,int num) if (S->top == max - 1 ) { printf ("栈满" ); return ; } S->top++; S->data[S->top] = num; } void pop (Stack* S, int * num) if (S->top == - 1 ) { printf ("栈空" ); return ; } *num = S->data[S->top]; S->top--; } void putstack (Stack* S) if (S->top == -1 ) { printf ("栈空" ); return ; } int i; for (i = 0 ; i <= S->top; i++) { printf ("%d" , S->data[i]); } } int main () Stack s; int num; int i; initStack(&s); for (i = 0 ; i < 11 ; i++) { push(&s, i); } putstack(&s); printf ("\n" ); for (i = 0 ; i < 5 ; i++) { pop(&s,&num); printf ("%d" , num); } }
两栈 就是用一个数组,包含两个栈,数组头和尾分别作为两个栈的初始栈顶。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 #include <stdio.h> #define max 10 typedef struct { int data[max]; int top1; int top2; }Stack; void initstack (Stack *S) S->top1 = -1 ; S->top2 = max; } void push (Stack* S, int num,int choice) if (S->top1 + 1 == S->top2) { printf ("栈满" ); return ; } if (choice == 1 ) { S->top1++; S->data[S->top1] = num; } if (choice == 2 ) { S->top2--; S->data[S->top2] = num; } return ; } void pop (Stack* S, int * num, int choice) if (choice == 1 ) { if (S->top1 == -1 ) { printf ("栈1空" ); return ; } S->top1--; *num = S->data[S->top1]; } if (choice == 2 ) { if (S->top2 == max) { printf ("栈2空" ); return ; } S->top2++; *num = S->data[S->top2]; } return ; } void putstack (Stack* S) if (S->top1 == -1 ) { printf ("栈空" ); return ; } int i; for (i = 0 ; i <= S->top1; i++) { printf ("%d" , S->data[i]); } printf ("\n" ); for (i = S->top2; i < max; i++) { printf ("%d" , S->data[i]); } } int main () Stack s; int i; int num; initstack(&s); for (i = 0 ; i < 3 ; i++) { push(&s, i, 1 ); push(&s, i, 2 ); } pop(&s, &num, 1 ); pop(&s, &num, 2 ); putstack(&s); }
栈链 用链表来构造栈结构,特点是可以随便push,这种链表没有表头,链表第一个就是栈顶。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 #include <stdio.h> #include "stdlib.h" typedef struct StackNode { int data; struct StackNode * next ; }StackNode, * LinkStackPtr; typedef struct { LinkStackPtr top; int count; }LinkStack; void InitLinkStack (LinkStack *ls) ls->count = 0 ; ls->top = NULL ; } void push (LinkStack* ls, int num) LinkStackPtr p; p = (LinkStackPtr)malloc (sizeof (StackNode)); p->data = num; p->next = ls->top; ls->top = p; ls->count++; } void pop (LinkStack* ls, int *num) LinkStackPtr p; *num = ls->top->data; p = ls->top; ls->top = ls->top->next; free (p); ls->count--; } void putLinkStack (LinkStack* ls) int i; LinkStackPtr p; p = ls->top; for (i = 0 ; i < ls->count;i++) { printf ("%d" , p->data); p = p->next; } } void freeLinkStack (LinkStack* ls) LinkStackPtr p,q; p = ls->top; while (p) { q = p->next; free (p); p = q; } ls->count = 0 ; } int main () LinkStack linkstack; int num; int i; InitLinkStack(&linkstack); for (i = 0 ; i < 5 ; i++) { push(&linkstack, i); } putLinkStack(&linkstack); pop(&linkstack, &num); printf ("\n%d\n" , num); putLinkStack(&linkstack); freeLinkStack(&linkstack); }
栈应用-递归 经典的斐波那契数列,也是走楼梯。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 #include <stdio.h> int fun (int num) if (num<2 ) { if (num==1 ) { return 1 ; } if (num==0 ) { return 0 ; } } return fun(num-1 )+fun(num-2 ); } int main () int num; num=fun(5 ); printf ("%d" ,num); }
还有就是四则运算用栈来实验,特别是如何利用栈来计算后缀表达式,和如何将中缀表达式转为后缀表达式,确实想出这个的人非常厉害,后面可以考虑实现一下。
队列 先进先出
普通队列 用一个数组来来创造队列,数组头作为对头,要插入数据就顺着数组插,要删除数据就从数组头开始删,这样的结构会导致删除后的数组头部分空间无法再次使用,所以就有了循环队列。
循环队列 使用head来标记头下标,用last来标记尾的下一个下标,为避免队列空和对列满的条件判断重合,故意让对列满时空一个元素,使对列满的条件改变。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 #include <stdio.h> #define max 10 typedef struct { int data[max]; int head; int last; }Queue; void initQueue (Queue *Q) Q->head = 0 ; Q->last = 0 ; } void push (Queue* Q,int num) if ((Q->last + 1 ) % max == Q->head) { printf ("对列满了\n" ); return ; } Q->data[Q->last] = num; Q->last=(Q->last+1 )%max; } void pop (Queue* Q, int * num) if (Q->head == Q->last) { printf ("对列空\n" ); return ; } *num = Q->data[Q->head]; Q->head = (Q->head + 1 ) % max; } int getlen (Queue* Q) return (Q->last - Q->head + max) % max; } void putQueue (Queue Q) int i,index; int len; len = getlen(&Q); if (len == 0 ) { printf ("队列为空\n" ); return ; } index = Q.head; for (i = 0 ;i<len;i++) { printf ("%d" , Q.data[index]); index = (index + 1 ) % max; } } int main () Queue Q; int i, num; initQueue(&Q); putQueue(Q); for (i = 0 ; i < 10 ; i++) { push(&Q, i); } pop(&Q, &num); printf ("%d\n" , num); putQueue(Q); }
用链表来实现对列 就是链表,用尾插来实现插入新元素,然后头删。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 #include <stdio.h> #include <stdlib.h> typedef struct QNode { int data; struct QNode * next ; }QNode,* QNodePtr; typedef struct { QNodePtr head; QNodePtr last; }LinkQueue; void initLinkQueue (LinkQueue* LQ) LQ->head = LQ->last= (QNodePtr)malloc (sizeof (QNode)); LQ->head->next = NULL ; } void push (LinkQueue* LQ, int num) QNodePtr p = (QNodePtr)malloc (sizeof (QNode)); p->data = num; p->next = NULL ; LQ->last->next = p; LQ->last = p; } void pop (LinkQueue* LQ, int * num) if (LQ->head == LQ->last) { printf ("队列空" ); return ; } QNodePtr p, q; q = LQ->head->next; *num = q->data; LQ->head->next = q->next; if (q == LQ->last) { LQ->last = LQ->head; } free (q); } int main () LinkQueue LQ; int i, num; initLinkQueue(&LQ); for (i = 0 ; i < 5 ; i++) { push(&LQ, i); } for (i = 0 ; i < 6 ; i++) { pop(&LQ,&num); } }
树 一些概念 树的定义 :树(Tree)是n(n≥0)个结点的有限集。n=0时称为空树。在任意一棵非空树中:(1)有且仅有一个特定的称为根(Root)的结点;(2)当n>1时,其余结点可分为m (m>0)个互不相交的有限集T1、T2、……、Tm,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree )。
结点的度 :结点拥有的子树数称为结点的度。度为0的结点称为叶节点或终端结点,就是尽头。度不为0的结点称为非终端结点或分支结点。
树的度 :树的度就算是树内各结点的度的最大值。
结点关系 :孩子,双亲,兄弟,堂兄。
树的深度或高度 :从根开始定义起,根为第一层,根的孩子为第二层,最大层就是深度。
有序树和无序数 :如果结点的子树左右不能变换,就是有序树,否则为无序树。
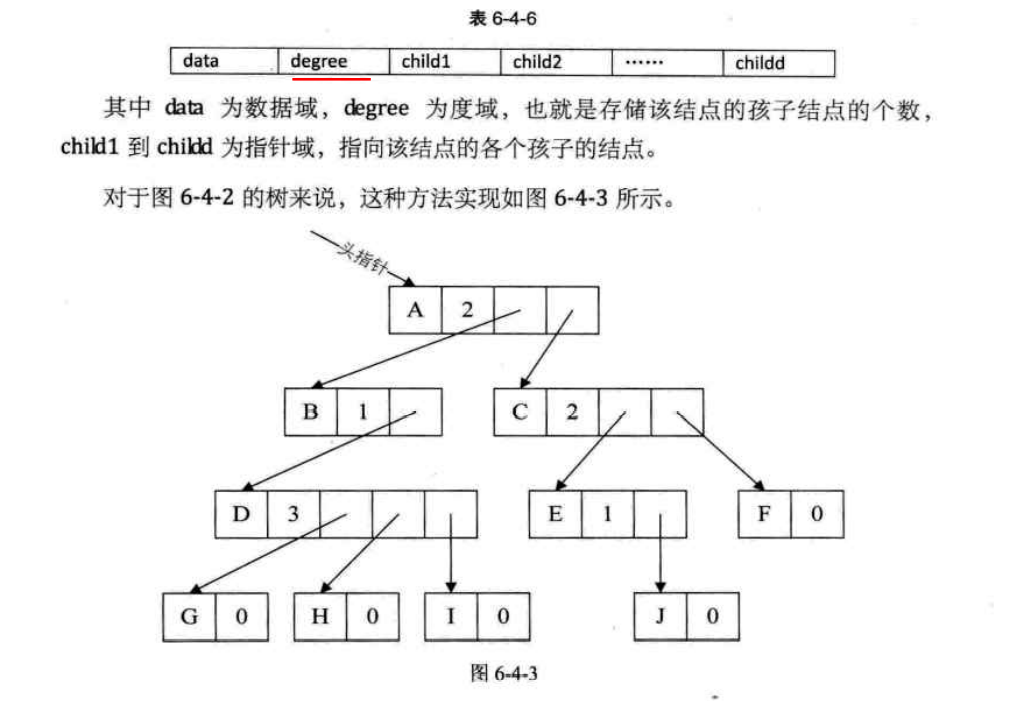
树的存储结构 由于树是1对多的关系,简单的顺序存储结构无法满足对树的要求,但是充分利用顺序存储和链式存储结构特点,就可以实现树的存储结构的表示。主要3种表示法:双亲表示法,孩子表示法,孩子兄弟表示法。
例子
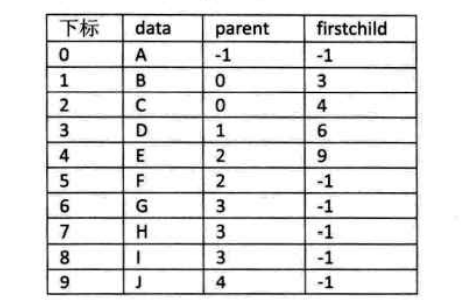
树的结构保证了除了根结点以外的所有结点,都会有双亲,所以我们可以定义下面的结构
1 2 3 4 5 6 7 8 9 10 11 12 13 #define max 100 typedef struct PTNode //结点结构{ int data; int parent; } typedef struct //树结构{ PTNode nodes[max]; int r,n; }PTree
根的parent就设置为-1,这样我们就可以通过任意结点找到其双亲。但是如果我们要找结点的孩子,就必须遍历整个结构。为解决这种情况,就可以在PTNode中添加一个firstchild,用来储存孩子的的下标,如果是叶节点,就将值设为-1。变成下面这种结构
2.孩子表示法
方案一:
采用多重链表表示法。
1 2 3 4 5 6 7 typedef struct { int data; int degree; Cboxptr box[degree]; }Cbox,*Cboxptr;
方案二:
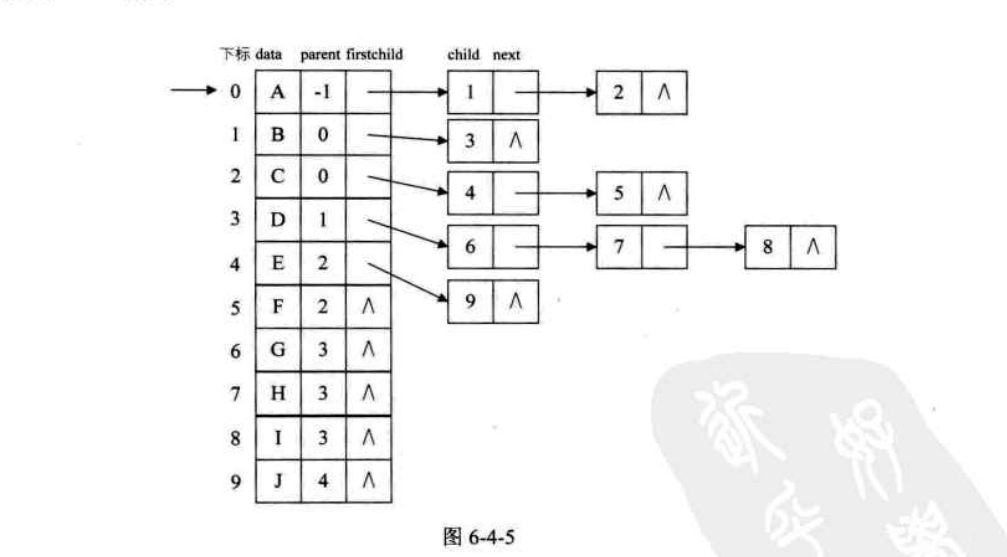
采用顺序储存结构和单链表相结合,将结点先用双亲表示法的顺序储存结构表示出来,然后添加一个指向第一个子结点的指针类型,所有子结点以单链表方式串起来。如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #define max 100 typedef struct CTNode { int child; struct CTNode *next ; }*ChildPtr; typedef struct { int data; ChildPtr firstchild; }CTBox; typedef struct { CTBox nodes[max]; int r,n; }CTree;
如果想要体验孩子的双亲,可以在CTbox结构中再添加parent变量,存储parent的下标,这种就算是双亲表示法的改进。
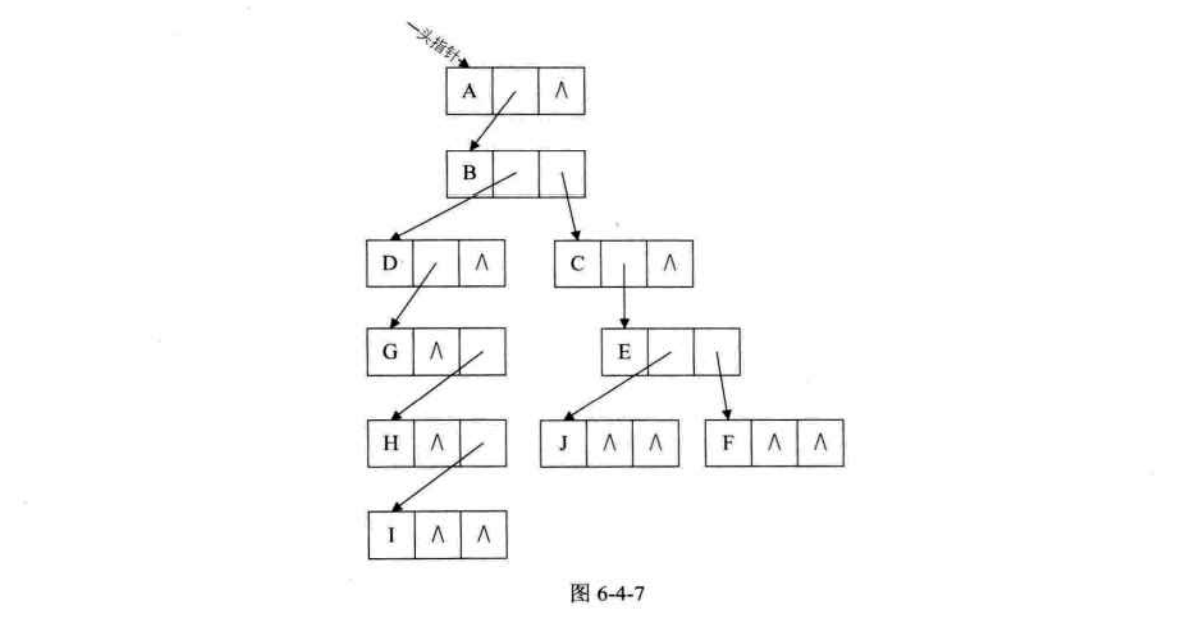
3.兄弟孩子表示法。
对于一个结点,如果其有子结点,那么第一个子结点就是唯一的,如果子结点有右兄弟,那么右兄弟也是唯一的。就可以定义出下面的结构。
1 2 3 4 5 6 typedef struct CSNode { int data; struct CSNode *firstchild ,*rightsib ; }CSNode,*CSTree;
得到如下结构
二叉树 通俗来讲就是最多只能有两个叉,而且左叉和右叉是不一样的。
然后主要是满二叉树和完全二叉树
满二叉树 :除了叶结点,其他结点都有两个叉,叶只能在最下一层,对称。
完全二叉树 :将二叉树写满编号,填满为满二叉树,编号顺序不能断。叶可在最下一层和倒数第二层,最底层的叶一定在左边。
二叉树性质 :二叉树性质
遍历二叉树 有很多遍历二叉树的方法
1.前序遍历
规则是若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。这种就是左子树优先级最高。
2.中序遍历
规则是若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。这种特点就是对于每个结点,其左子结点优先级比该结点高,改结点的优先级又比其右结点高。
3.后序遍历
规则是若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根结点。这种特点是叶子优先级最高,左叶又比右叶高。
而且关于二叉树的遍历还有个性质
已知前序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
已知后序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
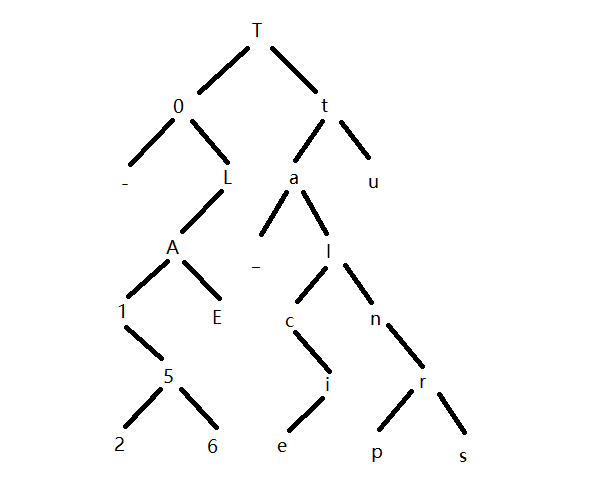
这种性质,还在2021 dozerctf的题中出现过,该题给了前序和中序,flag就是后序。我们可以来看看这道题。
前序遍历顺序:T0-LA1526Eta_lcienrpsu
中序遍历顺序:-01256AELT_aceilnprstu现在我们需要知道其后序遍历,所以我们要先还原树结构,根据不同遍历的特点,我们可以还原树结构如下。
中序遍历顺序:-2651EAL0-eicpsrnlautT二叉树的建立 给个二叉树链式结构,建立和遍历是差不多的,只是把输出,改为了赋值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 #include <stdio.h> #include <stdlib.h> int index = 0 ;char str[] = "ABD###C##" ;typedef struct BiTNode /* 结点结构 */{ char data; struct BiTNode * lchild , * rchild ; }BiTNode, * BiTree; void initBiTree (BiTree *T) *T = NULL ; } void CreateBiTree (BiTree *T) char ch; ch = str[index++]; if (ch == '#' ) { *T = NULL ; } else { (*T) = (BiTree)malloc (sizeof (BiTNode)); (*T)->data = ch; if (!*T) exit (0 ); CreateBiTree(&(*T)->lchild); CreateBiTree(&(*T)->rchild); } } void PreOrderTraverse (BiTree T) if (T == NULL ) { return ; } else { printf ("%c" , T->data); PreOrderTraverse(T->lchild); PreOrderTraverse(T->rchild); } } void InOrderTraverse (BiTree T) if (T == NULL ) { return ; } else { PreOrderTraverse(T->lchild); printf ("%c" , T->data); PreOrderTraverse(T->rchild); } } void PostOrderTraverse (BiTree T) if (T == NULL ) { return ; } else { PreOrderTraverse(T->lchild); PreOrderTraverse(T->rchild); printf ("%c" , T->data); } } void deleteBiTree (BiTree *T) if (*T) { deleteBiTree(&(*T)->lchild); deleteBiTree(&(*T)->rchild); free (*T); *T = 0 ; } } int main () BiTree T; initBiTree(&T); CreateBiTree(&T); PreOrderTraverse(T); printf ("\n" ); InOrderTraverse(T); printf ("\n" ); PostOrderTraverse(T); deleteBiTree(&T); }
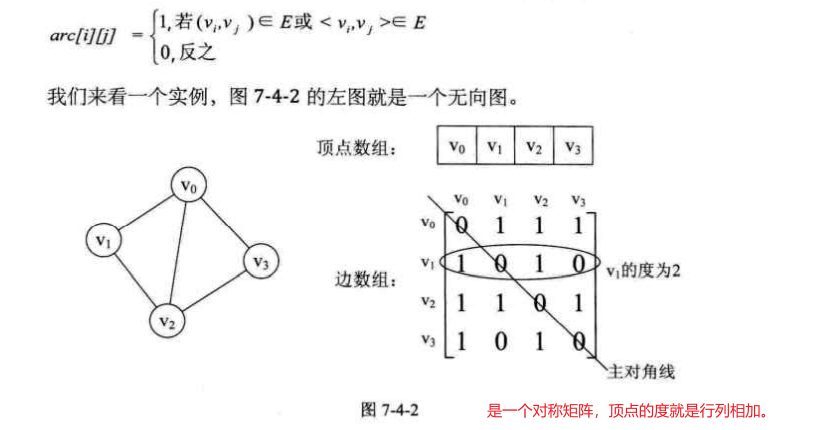
图 图的相关术语 图按照有无方向分为无向图 和有向图 。无向图由顶点和边构成,有向图由顶点和弧构成。弧有弧尾和弧头之分。
图按照边或弧的多少分稀疏图 和稠密图 。如果任意两个顶点之间都存在边叫完全图,有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。
图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度 ,有向图顶点分为入度 和出度 。
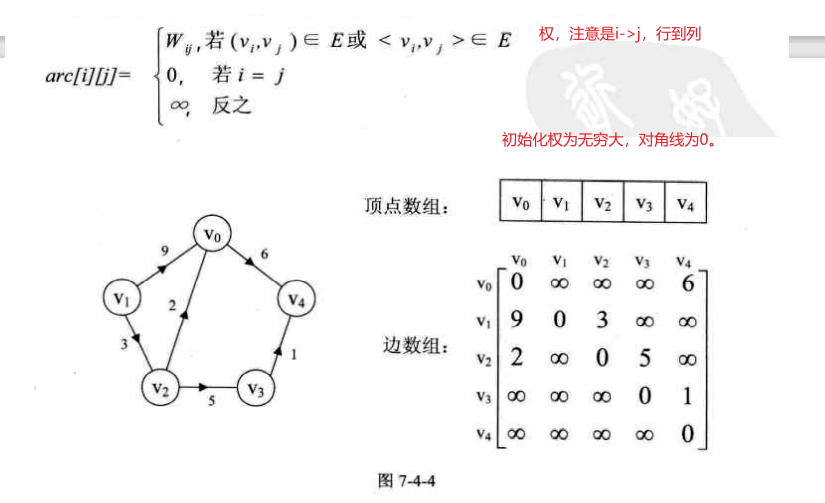
图上的边或弧上带权 则称为网 。
图中顶点间存在路径,两顶点存在路径则说明是连通的,如果路径最终回到起始点则称为环,当中不重复叫简单路径。若任意两顶点都是连通的,则图就是连通图,有向则称强连通图。图中有子图,若子图极大连通则就是连通分量,有向的则称强连通分量。
无向图中连通且n个顶点n-1条边叫生成树 。有向图中一顶点入度为0其余顶点入度为1的叫有向树。一个有向图由若干棵有向树构成生成森林。
图的存储结构 书上有5中方法,现在暂时记录两种。
1.邻接矩阵
对于无向图
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <stdio.h> #define MAXVEX 10 typedef struct { char vexs[MAXVEX]; int arc[MAXVEX][MAXVEX]; int numNodes, numEdges; }MGraph; void CreateMGraph (MGraph* G) int i,j,m,W; printf ("输入顶点数和边数:\n" ); scanf_s("%d,%d" , &G->numNodes, &G->numEdges); getchar(); printf ("请依次输入顶点名称:\n" ); for (i = 0 ; i < G->numNodes; i++) { scanf_s("%c" , &G->vexs[i],1 ); getchar(); } for (i = 0 ; i < G->numNodes; i++) for (j = 0 ; j < G->numNodes; j++) G->arc[i][j] = 65535 ; for (m = 0 ; m < G->numEdges; m++) { printf ("输入边(vi,vj)上的下标i,下标j和权w:\n" ); scanf_s("%d,%d,%d" , &i, &j, &W); G->arc[i][j] = W; } } void PutMGraph (MGraph G) int i, j; for (i = 0 ; i < G.numNodes; i++) { for (j = 0 ; j < G.numNodes; j++) { printf ("%6d" , G.arc[i][j]); } printf ("\n" ); } } int main () MGraph G; CreateMGraph(&G); PutMGraph(G); }
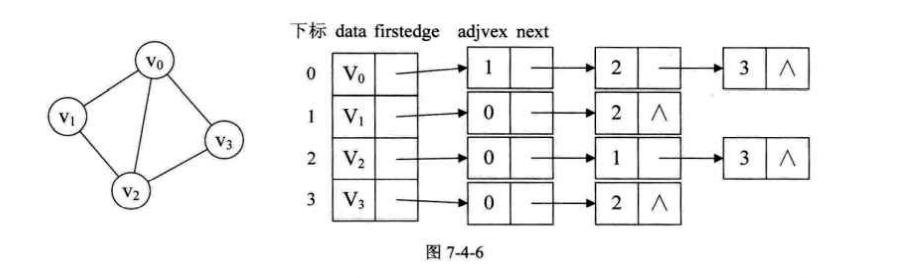
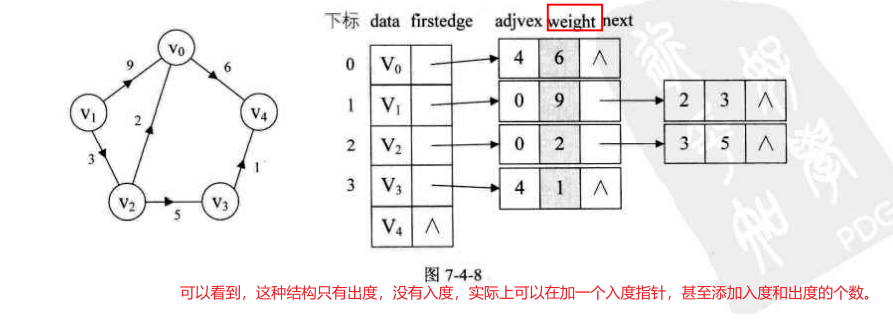
2.邻接表
上面的邻接矩阵在面对顶点多,边少的时候就会造成空间的浪费。邻接表就可以解决这一问题。
对于无向图
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 #include <stdio.h> #include <stdlib.h> #define MAXVEX 10 typedef struct EdgeNode /* 边表结点 */{ int adjvex; int info; struct EdgeNode * next ; }EdgeNode; typedef struct VertexNode /* 顶点表结点 */{ char data; EdgeNode* firstedge; }VertexNode, AdjList[MAXVEX]; typedef struct { AdjList adjList; int numNodes, numEdges; }GraphAdjList; void CreateALGraph (GraphAdjList* G) int i, j, m, W; EdgeNode *p,*q; printf ("输入顶点数和边数:\n" ); scanf_s("%d,%d" , &G->numNodes, &G->numEdges); getchar(); printf ("请依次输入顶点名称:\n" ); for (i = 0 ; i < G->numNodes; i++) { scanf_s("%c" , &G->adjList[i].data, 1 ); getchar(); G->adjList[i].firstedge = NULL ; } for (m = 0 ; m < G->numEdges; m++) { printf ("输入边(vi,vj)上的下标i,下标j和权w:\n" ); scanf_s("%d,%d,%d" , &i, &j, &W); p = (EdgeNode*)malloc (sizeof (EdgeNode)); p->adjvex = j; p->info = W; p->next = G->adjList[i].firstedge; G->adjList[i].firstedge = p; } } void freeALGraph (GraphAdjList G) int i; for (i = 0 ; i < G.numNodes; i++) { if (G.adjList[i].firstedge != NULL ); { EdgeNode *p,*q; p = G.adjList[i].firstedge; while (p) { q = p->next; free (p); p = q; } } } } int main () GraphAdjList G; CreateALGraph(&G); freeALGraph(G); }
遍历图 1.深度优先遍历。
就是一条路走到黑,发现不行就回走,找到可走的路径,然后走到底,如果不行就又回走,直到满足check条件。
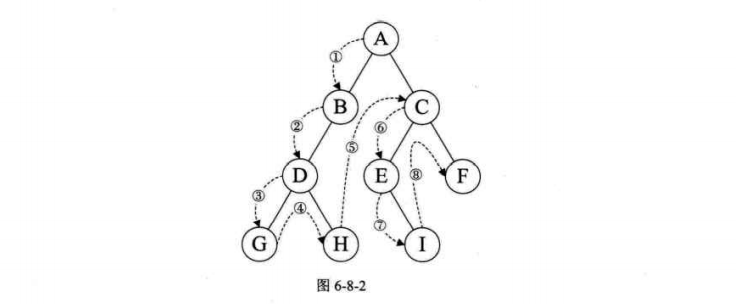
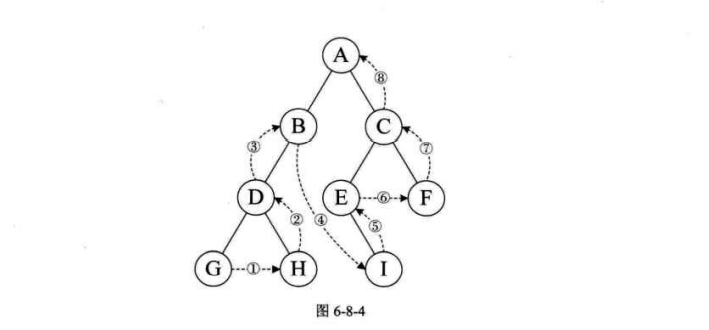
下面的例子为了方便,就直接将书中例子图复制过来了,主要是dfs搜索。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 #include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 typedef int Status; typedef int Boolean; typedef char VertexType; typedef int EdgeType; #define MAXSIZE 9 #define MAXEDGE 15 #define MAXVEX 9 #define INFINITY 65535 typedef struct { VertexType vexs[MAXVEX]; EdgeType arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; char mark[MAXVEX] = {0 };void CreateMGraph (MGraph* G) int i, j; G->numEdges = 15 ; G->numVertexes = 9 ; G->vexs[0 ] = 'A' ; G->vexs[1 ] = 'B' ; G->vexs[2 ] = 'C' ; G->vexs[3 ] = 'D' ; G->vexs[4 ] = 'E' ; G->vexs[5 ] = 'F' ; G->vexs[6 ] = 'G' ; G->vexs[7 ] = 'H' ; G->vexs[8 ] = 'I' ; for (i = 0 ; i < G->numVertexes; i++) { for (j = 0 ; j < G->numVertexes; j++) { G->arc[i][j] = 0 ; } } G->arc[0 ][1 ] = 1 ; G->arc[0 ][5 ] = 1 ; G->arc[1 ][2 ] = 1 ; G->arc[1 ][8 ] = 1 ; G->arc[1 ][6 ] = 1 ; G->arc[2 ][3 ] = 1 ; G->arc[2 ][8 ] = 1 ; G->arc[3 ][4 ] = 1 ; G->arc[3 ][7 ] = 1 ; G->arc[3 ][6 ] = 1 ; G->arc[3 ][8 ] = 1 ; G->arc[4 ][5 ] = 1 ; G->arc[4 ][7 ] = 1 ; G->arc[5 ][6 ] = 1 ; G->arc[6 ][7 ] = 1 ; for (i = 0 ; i < G->numVertexes; i++) { for (j = i; j < G->numVertexes; j++) { G->arc[j][i] = G->arc[i][j]; } } } void check (MGraph G) int i; int flag = 0 ; for (i = 0 ; i < G.numVertexes; i++) { if (mark[i] == 1 ) { flag = 1 ; } else { flag = 0 ; break ; } } if (flag == 1 ) { printf ("\nsecess!" ); } } void dfs (MGraph G,int i) int m; mark[i] = 1 ; printf ("%c" , G.vexs[i]); check(G); for (m = 0 ; m<G.numVertexes; m++) { if (mark[m] != 1 && G.arc[i][m]==1 ) { dfs(G, m); } } } int main (void ) MGraph G; CreateMGraph(&G); dfs(G,0 ); return 0 ; }
还有种很典型的迷宫dfs例子,ctf中也经常用到,下面代码写的比较重复,是可以用一个for循环来代替的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 #include <stdio.h> #include <stdlib.h> char map [5 ][5 ] = { {'#' ,'#' ,'#' ,'#' ,'#' }, {'#' ,'0' ,'0' ,'0' ,'#' }, {'#' ,'0' ,'#' ,'0' ,'#' }, {'0' ,'0' ,'#' ,'0' ,'2' }, {'#' ,'0' ,'0' ,'0' ,'#' }, }; int mark[5 ][5 ] = { 0 };char way[100 ];int index = 0 ;void check (int x,int y) if (map [x][y] == '2' ) { printf ("way: %s\n" , way); } } void dfs (int x,int y) int xnew=0 , ynew=0 ; check(x, y); xnew = x - 1 ; ynew = y; if (xnew >= 0 && xnew < 5 && ynew >= 0 && ynew < 5 && map [xnew][ynew] != '#' && mark[xnew][ynew] != 1 ) { way[index++] = 'w' ; mark[x][y] = 1 ; dfs(xnew, ynew); mark[x][y] = 0 ; way[--index] = ' ' ; } xnew = x; ynew = y + 1 ; if (xnew >= 0 && xnew < 5 && ynew >= 0 && ynew < 5 && map [xnew][ynew] != '#' && mark[xnew][ynew] != 1 ) { way[index++] = 'd' ; mark[x][y] = 1 ; dfs(xnew, ynew); mark[x][y] = 0 ; way[--index] = ' ' ; } xnew = x + 1 ; ynew = y; if (xnew >= 0 && xnew < 5 && ynew >= 0 && ynew < 5 && map [xnew][ynew] != '#' && mark[xnew][ynew] != 1 ) { way[index++] = 's' ; mark[x][y] = 1 ; dfs(xnew, ynew); mark[x][y] = 0 ; way[--index] = ' ' ; } xnew = x; ynew = y - 1 ; if (xnew >= 0 && xnew < 5 && ynew >= 0 && ynew < 5 && map [xnew][ynew] != '#' && mark[xnew][ynew] != 1 ) { way[index++] = 'a' ; mark[x][y] = 1 ; dfs(xnew, ynew); mark[x][y] = 0 ; way[--index] = ' ' ; } } int main () int i, j; for (i = 0 ; i < 5 ; i++) { for (j = 0 ; j < 5 ; j++) { printf ("%c" , map [i][j]); } printf ("\n" ); } dfs(3 , 0 ); }
极客巅峰一道maze题也用到了dfs,python写的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 from pwn import *io = process('./maze1' ) next = [[1 , 0 ], [0 , -1 ],[0 , 1 ], [-1 , 0 ]]way = "SADW" back = {'W' : 'S' , 'S' : 'W' , 'A' : 'D' , 'D' : 'A' } ans = '' flag = [0 ] * 1000 def putstr (a ): ans = '' for i in a: if (i == 0 ): break ans += i print(ans) def dfs (x, y, step ): putstr(flag) for i in range (4 ): xnew = x + next [i][0 ] ynew = y + next [i][1 ] flag[step] = way[i] flag[step+1 ] = 0 if (maze[xnew][ynew] == 1 or mark[xnew][ynew]==1 ): continue io.sendline(way[i]) ans = io.readline() if (ans == b'1\n' ): maze[xnew][ynew] = 0 mark[x][y] = 1 dfs(xnew, ynew, step + 1 ) io.sendline(back[way[i]]) io.readline() mark[x][y] = 0 elif (ans[0 :4 ]==b"Good" ): print("success" ,end=':' ) putstr(flag) else : maze[xnew][ynew] = 1 maze = [[0 for i in range (1000 )] for j in range (1000 )] mark = [[0 for i in range (1000 )] for j in range (1000 )] io.recvuntil("This is the beginning. You can only go south.\n" ) dfs(3 , 3 , 0 )
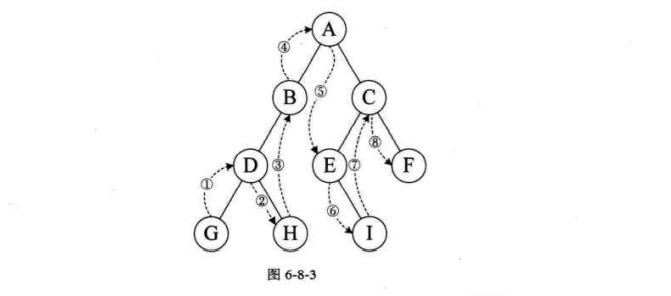
2.广度优先bfs
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 #include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 typedef int Status; typedef int Boolean; typedef char VertexType; typedef int EdgeType; #define MAXSIZE 9 #define MAXEDGE 15 #define MAXVEX 9 #define INFINITY 65535 typedef struct { VertexType vexs[MAXVEX]; EdgeType arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; char mark[MAXVEX] = { 0 };#define max 10 typedef struct { int data[max]; int head; int last; }Queue; void initQueue (Queue* Q) Q->head = 0 ; Q->last = 0 ; } void push (Queue* Q, int num) if ((Q->last + 1 ) % max == Q->head) { printf ("对列满了\n" ); return ; } Q->data[Q->last] = num; Q->last = (Q->last + 1 ) % max; } void pop (Queue* Q, int * num) if (Q->head == Q->last) { printf ("对列空\n" ); return ; } *num = Q->data[Q->head]; Q->head = (Q->head + 1 ) % max; } int QueueEmpty (Queue Q) if (Q.head == Q.last) { return 1 ; } else { return 0 ; } } int getlen (Queue* Q) return (Q->last - Q->head + max) % max; } void CreateMGraph (MGraph* G) int i, j; G->numEdges = 15 ; G->numVertexes = 9 ; G->vexs[0 ] = 'A' ; G->vexs[1 ] = 'B' ; G->vexs[2 ] = 'C' ; G->vexs[3 ] = 'D' ; G->vexs[4 ] = 'E' ; G->vexs[5 ] = 'F' ; G->vexs[6 ] = 'G' ; G->vexs[7 ] = 'H' ; G->vexs[8 ] = 'I' ; for (i = 0 ; i < G->numVertexes; i++) { for (j = 0 ; j < G->numVertexes; j++) { G->arc[i][j] = 0 ; } } G->arc[0 ][1 ] = 1 ; G->arc[0 ][5 ] = 1 ; G->arc[1 ][2 ] = 1 ; G->arc[1 ][8 ] = 1 ; G->arc[1 ][6 ] = 1 ; G->arc[2 ][3 ] = 1 ; G->arc[2 ][8 ] = 1 ; G->arc[3 ][4 ] = 1 ; G->arc[3 ][7 ] = 1 ; G->arc[3 ][6 ] = 1 ; G->arc[3 ][8 ] = 1 ; G->arc[4 ][5 ] = 1 ; G->arc[4 ][7 ] = 1 ; G->arc[5 ][6 ] = 1 ; G->arc[6 ][7 ] = 1 ; for (i = 0 ; i < G->numVertexes; i++) { for (j = i; j < G->numVertexes; j++) { G->arc[j][i] = G->arc[i][j]; } } } void bfs (MGraph G) int i, j; Queue Q; initQueue(&Q); for (i = 0 ; i < G.numVertexes; i++) { if (mark[i] != 1 ) { mark[i] = 1 ; printf ("%c" , G.vexs[i]); push(&Q, i); while (!QueueEmpty(Q)) { pop(&Q, &i); for (j = 0 ; j < G.numVertexes; j++) { if (G.arc[i][j] == 1 && mark[j] != 1 ) { mark[j] = 1 ; printf ("%c" , G.vexs[j]); push(&Q, j); } } } } } } int main (void ) MGraph G; CreateMGraph(&G); bfs(G); return 0 ; }